いろいろ ピタゴラス の 定理 直角 三角形 221119-ベク��ル 直交 完備 ピタゴラス

Web連載 ピラミッドの謎 4 2 ピタゴラスの定理 マテマティカ

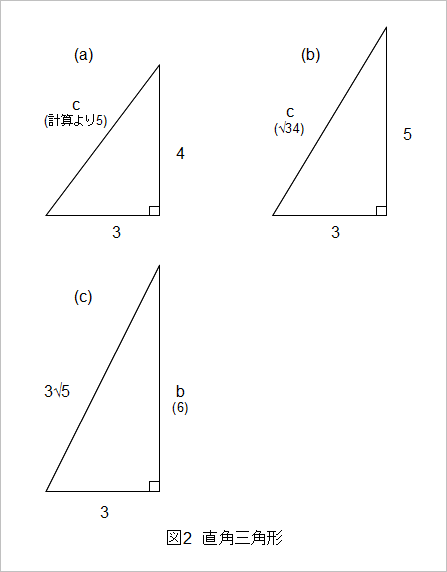
Web じつは、三平方の定理（ピタゴラスの定理）のすごいところは、 直角三角形の2辺の長さがわかれば、残りの辺の長さがわかる ってところなんだ。 たとえば、斜辺の長さ13cm、その他一辺の長さが5cmの直角三角形DEFがあったとしよう。Web3 辺の長さが 3：4：5 の直角三角形 上の三角形は、2 つの辺の長さが 3 cm と 4 cm で、その間の角が 90° である直角三角形です。 このように、直角三角形の2辺の長さが分かっていれば

ベクトル 直交 完備 ピタゴラス

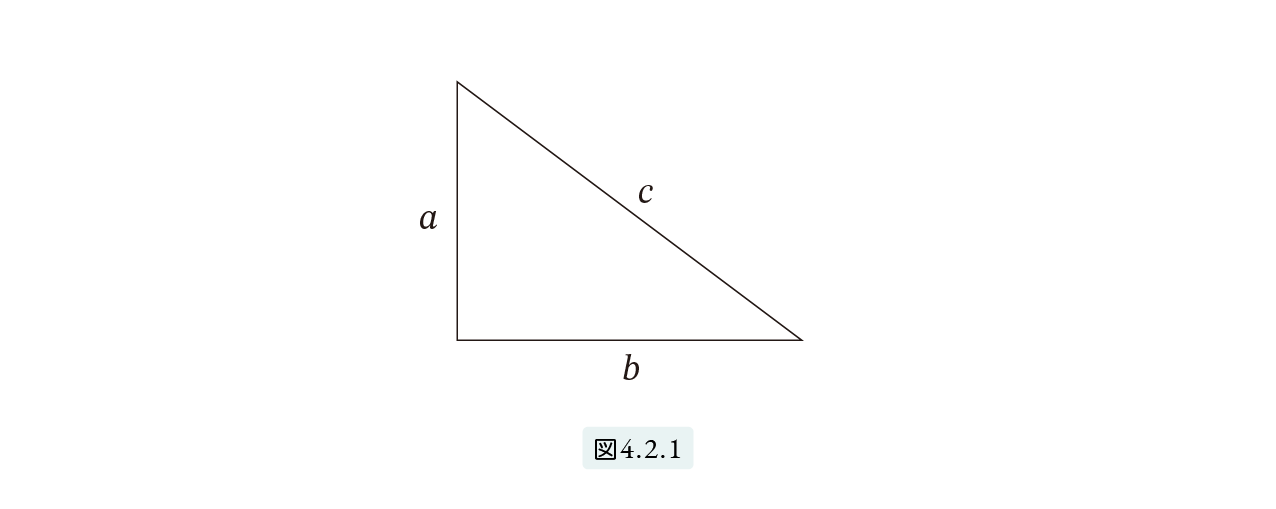
ベクトル 直交 完備 ピタゴラス-Webピタゴラスの定理を、ギリシアの概念だけを使って述べなおすと次のようになります。 定理 421 (ピタゴラスの定理) 図421 の直角三角形において、次が成立する。 2 ( a ) ＋ 2 ( b ) ＝Webピタゴラスの三角形 とは， 各辺の長さの比 abc が自然数となるような， 作図に都合のよい直角三角形のことだ． 表． ピタゴラスの三角形の一覧 （ただし，a ≦ b ≦ c ≦ 100 の範囲の

3分で分かる 三平方の定理の公式と証明 使い方をわかりやすく 合格サプリ

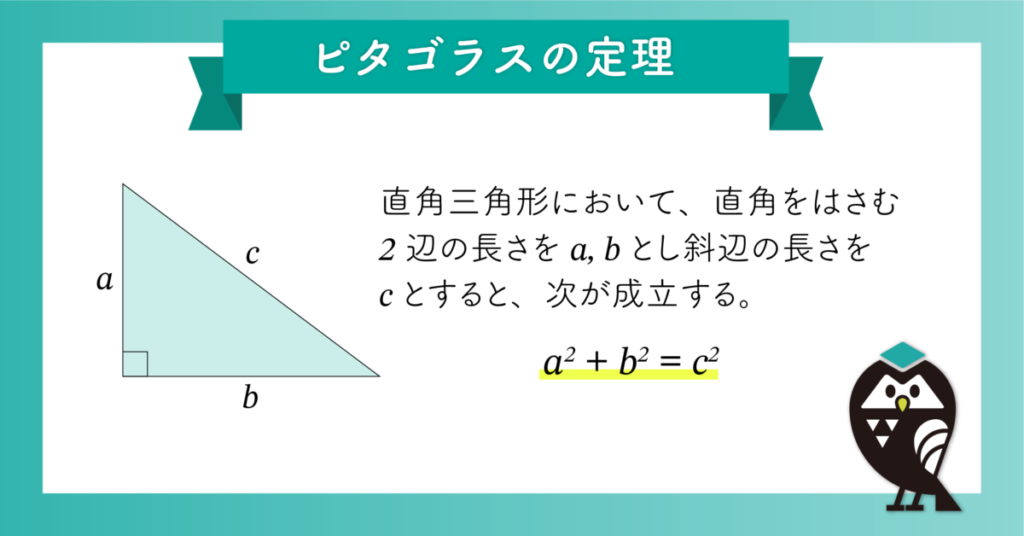
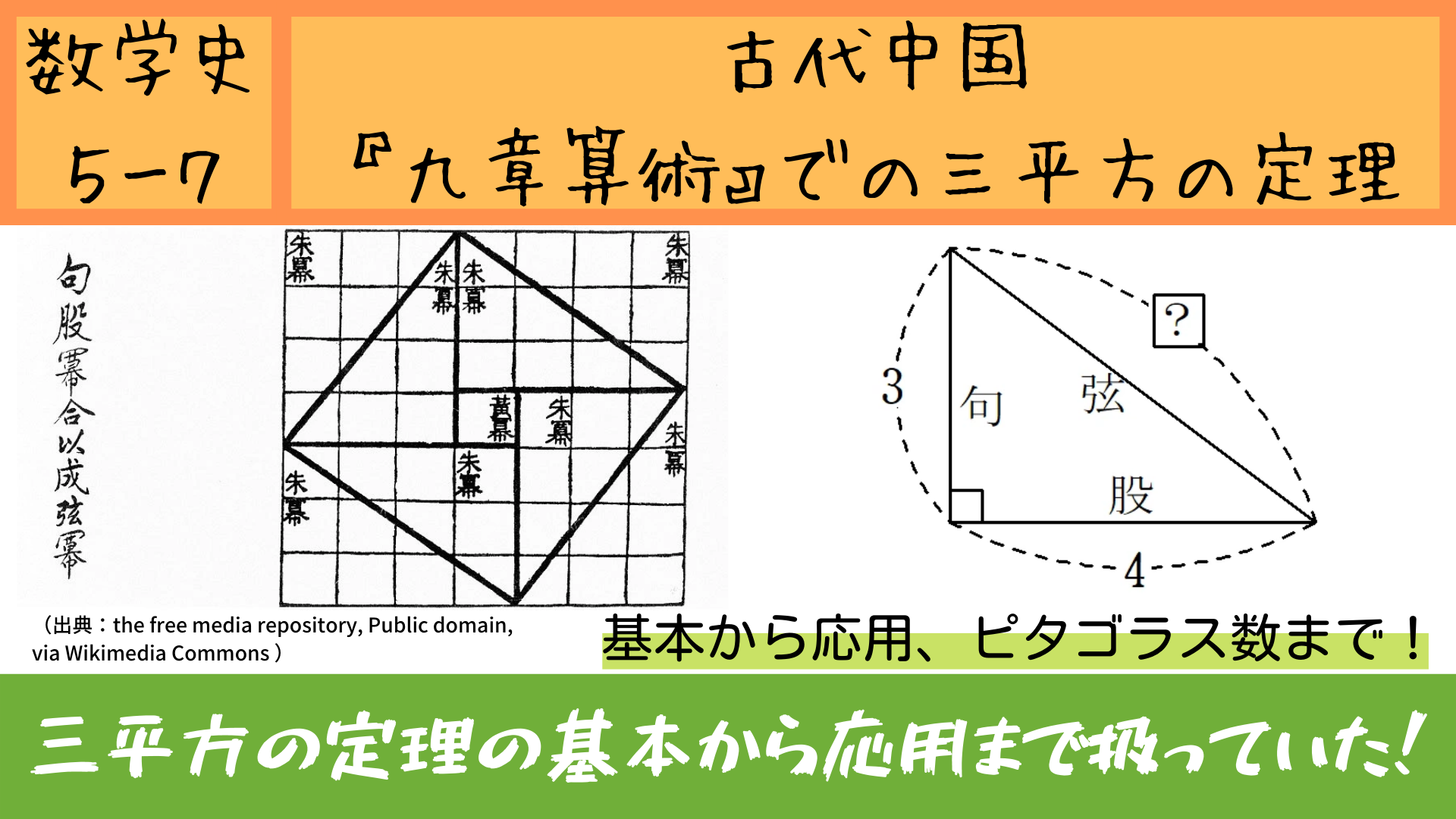
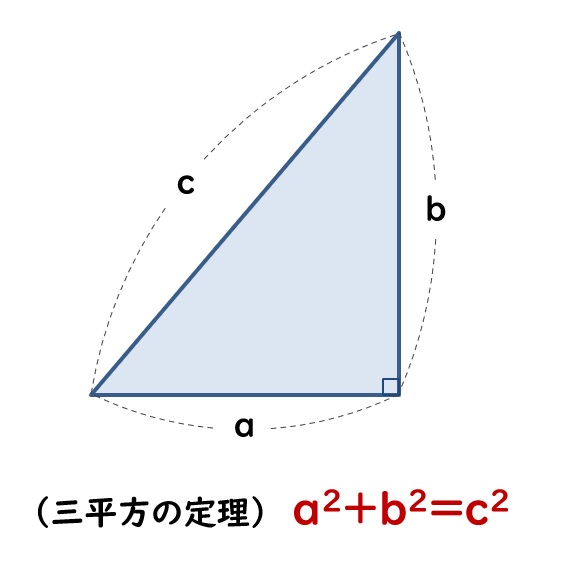
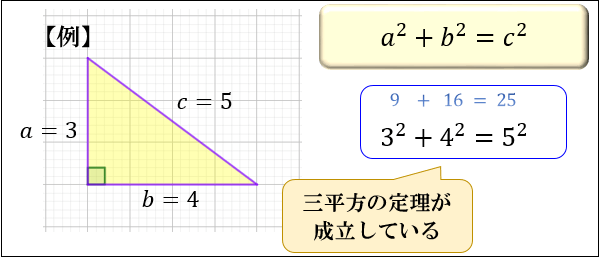
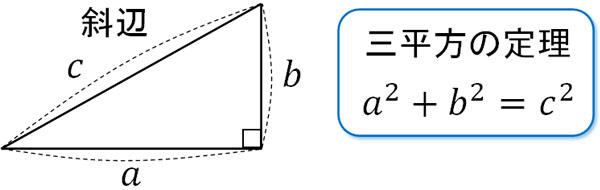
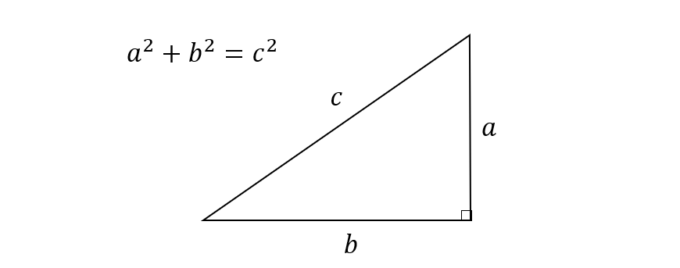
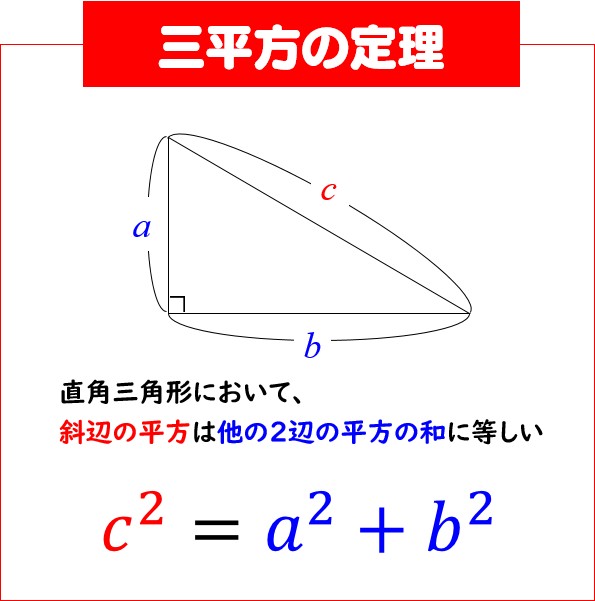
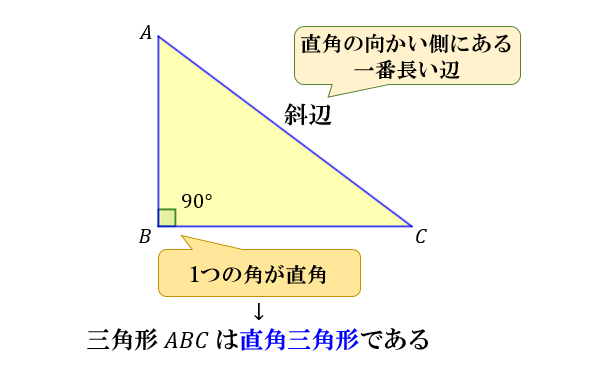
Webまた、よく知られているように直角三角 形の3辺の間には、ピタゴラスの定理(定理 1)が成り立つことを授業で学習した。 定理1 (ピタゴラスの定理) 直角を挟む2辺の長さがx, yである直角 三Web三平方の定理（ピタゴラスの定理) 三平方の定理（ピタゴラスの定理） 直角三角形において， a^2b^2=c^2 a2 b2 = c2 つまり「斜辺以外の二辺の長さの二乗の和」は「斜辺の二乗」とWeb ピタゴラスは遅かった 三平方の定理「最古の応用例」 畑の図面が記されている粘土板。 三平方の定理を使って面積や形が正確に描かれている

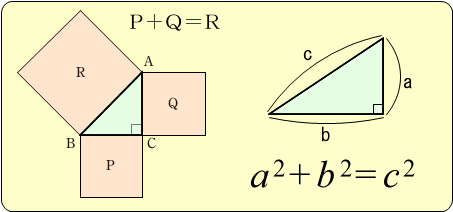
Webこれで, 直角三角形でなくても, ピタゴラスの定理を用いて残った辺の長さが決定できました。導出された数式はまさに余弦定理です。なお, 本回答は math\\theta/math が鋭角の場合でWeb直角三角形の選択した2つの入力値から他の要素の値を計算します。 b= √a2h2 θ=tan−1(h a) S = 1 2ah b = a 2 h 2 θ = t a n − 1 ( h a) S = 1 2 a h 入力指定 底辺と高さ 底辺と斜辺 底辺とWebこれは、ピタゴラスの定理の証明の時に使う等積変形を一般化したものといえます。 (2)一般の三角形でも同じ様なことがいえないか 余弦定理 次は「一般化」という拡張です。 つまり、

ベクトル 直交 完備 ピタゴラスのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

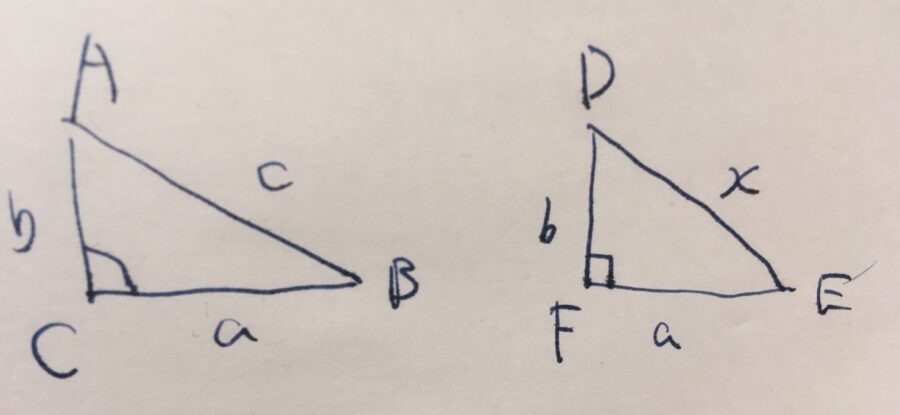「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。

Webピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。 例えば、 直交座標系 において原点と任意の点を結ぶ線分Webブリタニカ国際大百科事典 小項目事典 ピタゴラスの定理の用語解説 三平方の定理ともいう。直角三角形において，直角である頂角の対辺の長さの平方は，他の2辺の平方の和に等しい

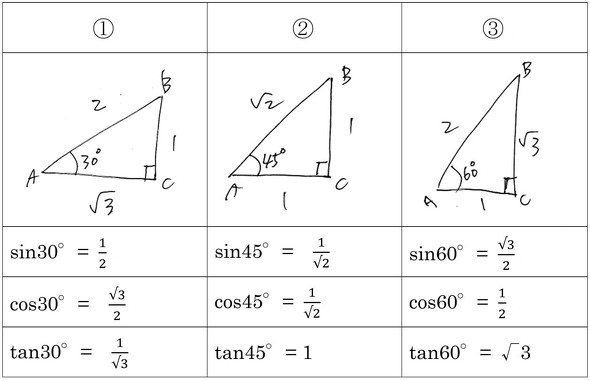
Incoming Term: ピタゴラスの定理 1 2 ルート3, ベクトル 直交 完備 ピタゴラス, 黄金比 ピタゴラスの定理 フィボナッチ数列 ケプラー三角形,